国密算法SM2与ECDSA和RSA比较

在数字签名中,一般先将消息进行杂凑运算,生成较短的、固定长度的杂凑值,然后使用一种签名算法对杂凑值进行签名。因此,必须在数字签名中排除杂凑算法的干扰。本文将对SM2算法、ECDSA算法、RSA算法应用于数字签名的算法性能进行比较。
SM2、ECDSA与RSA
1985年,ECC被首次提出,该算法具有重要的理论研究价值和广阔的应用前景,近年来已成为公钥密码领域的研究热点。ECDSA与SM2属于ECC数字签名算法,RSA是目前较容易理解和实现的公钥算法,在电子商业中被广泛使用。
SM2数字签名算法与ECDSA算法均基于ECC上的离散对数困难问题,均由系统参数和辅助函数选取、签名算法、签名验证算法3个步骤组成。两种算法的整体结构相似,主要区别如下。
1)椭圆曲线的选取不同;
2)杂凑函数选取不同;
3)处理待签名消息的方式不同;
4)签名计算方式不同。
数字签名算法计算量
SM2数字签名算法与ECDSA算法的整体结构相似,主要区别是杂凑函数的选取与签名的计算方式不同。考虑数字签名算法直接对杂凑值进行签名与签名验证,因此在对SM2数字签名算法与ECDSA算法进行计算量分析时,不计入杂凑值的计算量。
在签名算法、签名验证算法两个步骤中,两种算法均使用了椭圆曲线上的运算和有限域上的模运算。对两种算法的总体运算量做具体统计分析,将有限域上的模加运算记为MA,将模逆运算记为MI,将模乘运算记为MM,将取模运算记为MO,将椭圆曲线上的倍点运算记为MP,将点加运算记为AP,得到SM2与ECDSA的数字签名计算量对比如表1所示。
表1 SM2与ECDSA的数字签名计算量对比
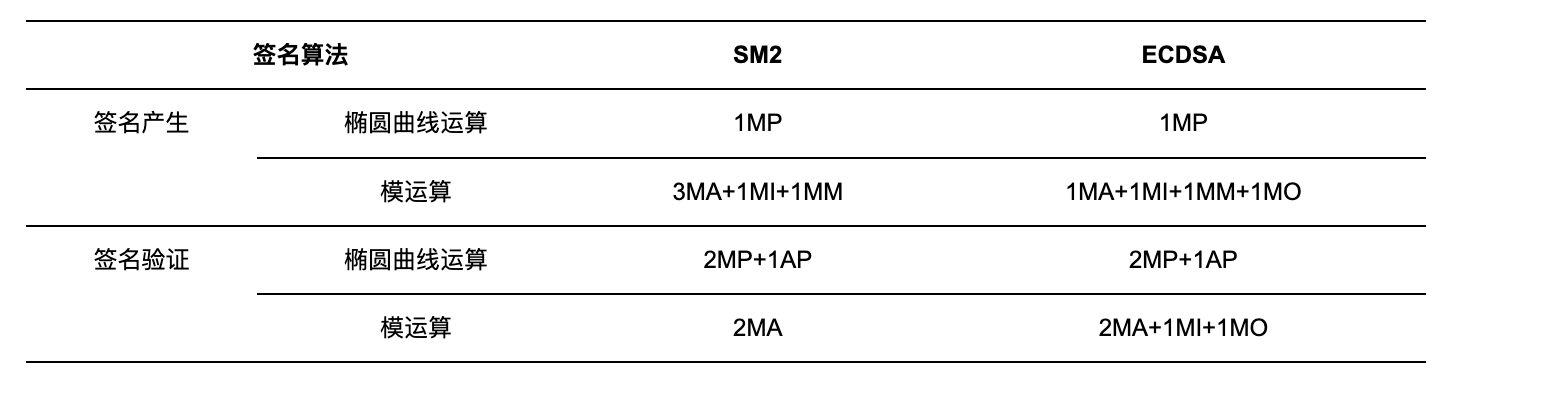
由表1可知,不考虑杂凑值的计算量时,SM2数字签名算法的签名产生与签名验证计算量均与ECDSA相近。
数字签名算法性能测试分析
对SM2数字签名算法、ECDSA和RSA数字签名算法进行性能测试,循环次数N=1000。为保持安全强度的一致性,ECDSA算法的杂凑函数选用SHA-256。
1)去除杂凑算法对签名的影响
将杂凑算法运算耗时去除,对两种算法进行软件性能测试。将256 bit长度的随机数据模拟为由SM3和SHA-256产生的摘要值,作为SM2数字签名算法和ECDSA的输入,对该摘要数据进行签名及签名验证运算。
不计杂凑算法耗时在内的签名耗时比如表2所示,其中ECDSA_secp256k1表示ECDSA选取曲线secp256k1,此曲线为比特币所选择的曲线;ECDSA_X9.62prime256v1表示ECDSA选取曲线X9.62prime256v1,此曲线为EMV选择的NIST公布的曲线;SM2选取默认建议曲线。
表2 不计杂凑算法耗时在内的签名耗时比

由表2可知,不计杂凑值耗时,在一般情况下(如ECDSA选取曲线secp256k1),OpenSSL SM2数字签名算法与ECDSA的签名和签名验证耗时相近,这与算法计算量分析结论相符。
此外,由于OpenSSL工具套件对X9.62prime256v1曲线做了算法层面的快速实现,使得ECDSA在选取此曲线时,数字签名性能得到大幅度提升。
2)杂凑算法对签名的影响
对不含杂凑运算的数字签名耗时测试能够验证算法的计算量理论分析结论,一个完整的数字签名过程包含对消息M的杂凑运算和对杂凑值数字签名运算两部分,杂凑运算会对签名算法的整体耗时产生影响。因此,对包含杂凑运算耗时在内的数字签名算法性能进行测试,在15组不同输入长度情况下,计算SM2数字签名算法、ECDSA(使用曲线secp256k1)、RSA算法的运行耗时比。其中,对RSA算法的2048 bit(当前各类系统中最常用的密钥长度,具有实际参考价值)和3072 bit(与SM2和ECDSA安全强度相当)密钥长度进行测试。3种数字签名算法的签名运算时间比如图1所示,3种数字签名算法的签名验证运算时间比如图2所示。
图1 3种数字签名算法的签名运算时间比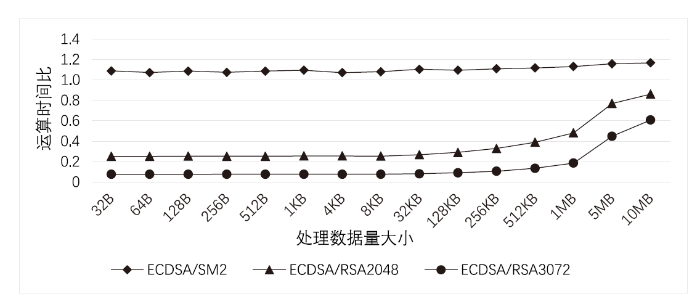
图2 3种数字签名算法的签名验证运算时间比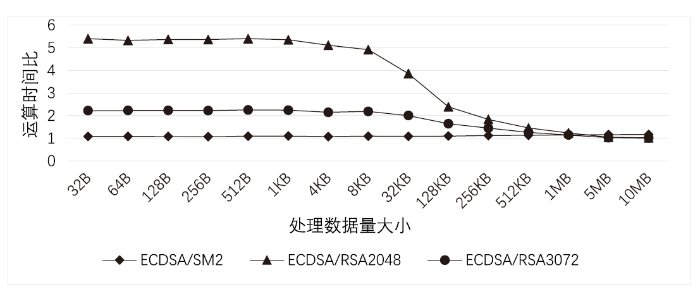
由图1和图2可以看出,SM2数字签名算法和ECDSA (两者均属于ECC算法)的签名速度比RSA快,但签名验证比RSA慢。
此外,对于ECDSA和SM2数字签名算法,随着输入数据量的增多,最终两种算法签名和签名验证的效率比接近其所使用的杂凑函数效率比。当数据量较多时,杂凑函数的运算量在数字签名算法整体运算中占比很高,因此杂凑计算的开销成为算法的主要开销。
3)优化对算法性能的影响
目前,A厂商针对国密算法进行了专项优化,对SM2算法优化前后的性能进行对比测试,测试SM2数字签名算法、ECDSA、RSA算法的签名与签名验证的绝对运算速度与平均运算速度比(以RSA2048为标准)的对比情况,SM2、ECDSA、RSA绝对运算速度如图3所示,SM2、ECDSA、RSA运算速度比如图4所示。
图3 SM2、ECDSA、RSA绝对运算速度
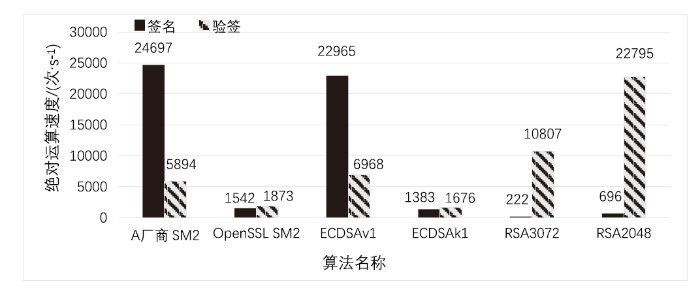
图4 SM2、ECDSA、RSA运算速度比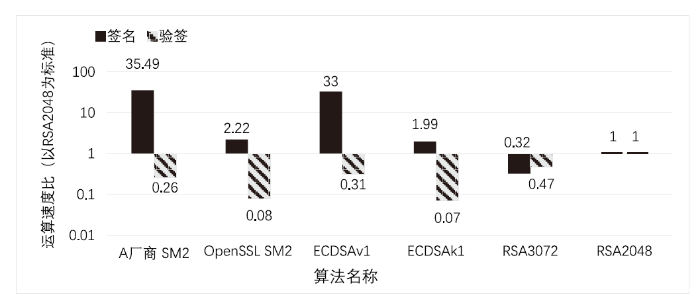
由图3和图4可以看出,A厂商对SM2算法的优化使实际使用性能得到了大幅度提升,签名运算速度是OpenSSL SM2的16倍、是NIST P256曲线的1.08倍、是同安全级别RSA的110倍。签名验证运算速度是OpenSSL SM2的3倍、是NIST P256曲线的0.84倍、是同级别RSA的0.55倍。从原理上来说,ECC类算法签名验证运算速度比RSA慢,测试数据也证明了该结论。
由上述测试结果分析可知,当不含杂凑运算开销时,SM2数字签名算法和ECDSA的性能相近;当杂凑运算包含在内时,随着数据量的增多,SM2数字签名算法和ECDSA的性能之比逐渐接近于SM3和SHA-256的性能之比。
在实际应用中,经过优化后的SM2性能得到了大幅度提升。从绝对数值方面来看,SM2中较慢的签名运算速度远高于RSA中较慢的签名运算速度,在同时需要使用签名和签名验证的场景中,优化后的SM2会更占优势。


